Contents

• Introduction
• Getting the data
• Fitting a Gaussian
• The most Gaussian names
  • Attempt 1
  • Attempt 2
• The least Gaussian names

Introduction

A few years ago I was looking at plots of occurences through time with a friend, when we spotted something "oddly Gaussian":

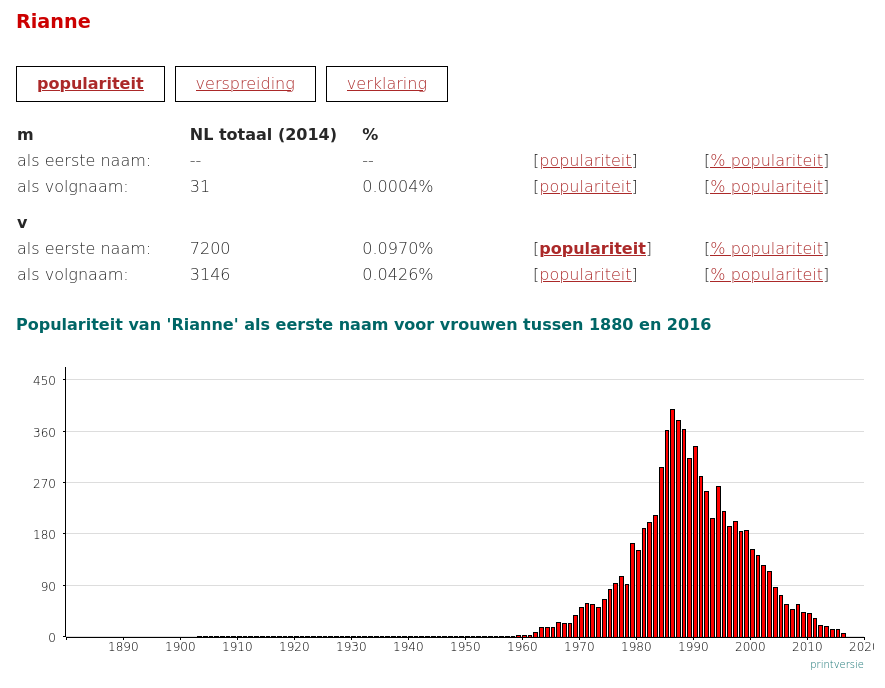Source: Meertens Voornamenbank

Being surrounded by Gaussian Distributions while taking a Machine Learning course taught by Rianne van den Berg, we wondered if "Rianne" was the most Gaussian name. That would be fitting.

Getting the data

A few months ago I decided to finally satisfy my curiosity. While downloading all available name graphs, I had to take some pre-processing decisions:

• Only first names count, not second, third, or nth names where n>3.
• On the KNAW website there are separate plots for men/women. I simply added the count values per year.
• The data on the KNAW website is not accurate for rare names, for privacy reasons. I discarded names with fewer than 150 occurences in the top year for that name. (experimentally determined).

Fitting a Gaussian

It's easy to fit a a function like a 1-dimensional Gaussian using for instance scipy's curve_fit.

This is the result for the name Anna. The mean is the year 1935.04 and the standard deviation is 26.95 years:

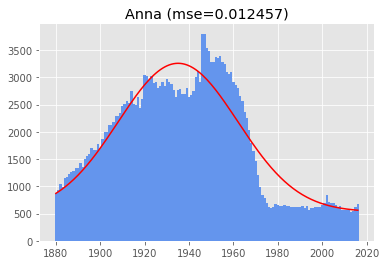
As you can see, my name is not very Gaussian. The (normalized) mean squared error to the true distribution is pretty high, considering all the best names I found have MSE's smaller than 0.001.

The most Gaussian names

Attempt 1

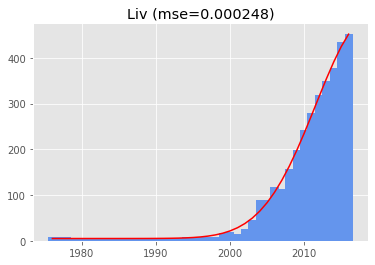
When simply looking at MSE, it turns out the most Gaussian name is.... Liv:

Looking at the runner-ups, it turns out it's easier to get a good fit when your data is a one-tailed Gaussian:

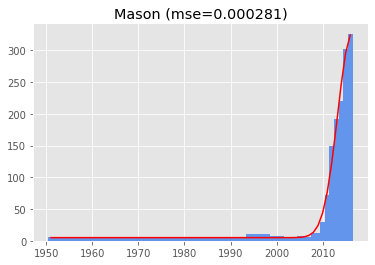
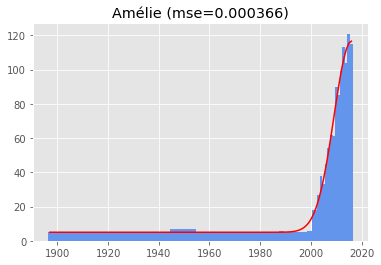
While it is true that as of 2020, these names best fit a Gaussian distribution because we don't know the future, this is not entirely what I had in mind. And the one-tailed Gaussians make up most of the top 50.

We can add another criterion to really find those Gaussian-looking names like Rianne.

• The mean + sd has to be smaller than the maximum year in which the name was given.
• The mean - sd has to be greater than the minimum year in which the name was given. (For completeness, this rarely occurs in the real data)

The name "Liv" does not satisfy this criterion, since its corresponding Gaussians mean is 2018 and its standard deviation 7, bringing us to 2026 for the other side of the tail.

Attempt 2

After this adjustment, the Gaussians look more two-tailed and better in general.

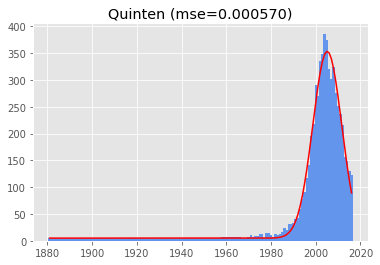
I proudly present, the most Gaussian name in the Netherlands, with a MSE of 0.00057: Quinten!

The three runner-ups are as follows:

• 2) Thijmen
• 3) Koen
• 4) Jente

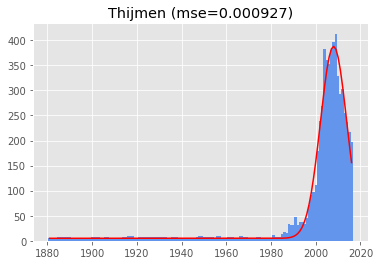
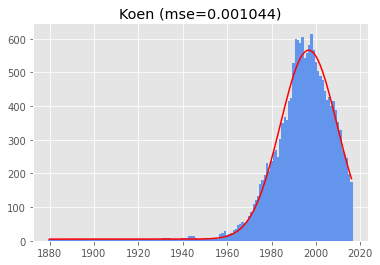
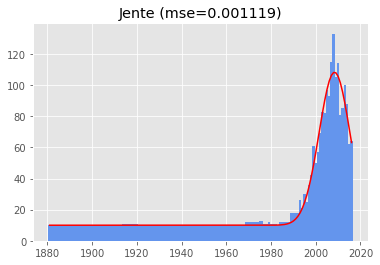
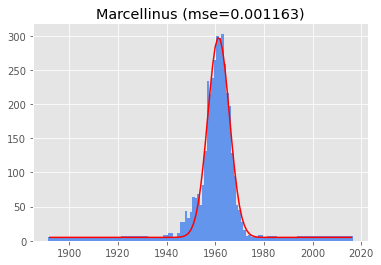
These still look suspiciously wanting to be one-tailed. Marcellinus is in fifth place, and the first one to look TRULY two-tailed, with a mean of 1961:

• 5) Marcellinus

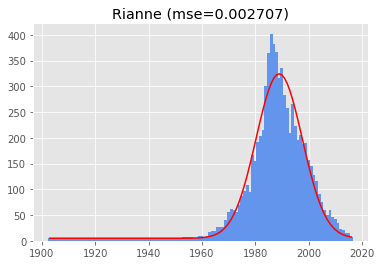
The real question is, is Rianne very Gaussian? Or did we just deceive ourselves thinking a teacher of Gaussians would be relatively very Gaussian?

The good news is that Rianne is in the top 100 out of 630 names that fit my criteria. The Gaussian fit is at spot 69 with an MSE of 0.00271:

• 69) Rianne

The Least Gaussian Names

If you're wondering, the two least Gaussian names that still have a standard deviation + mean within range

• 630) Renee

• 631) Sophia

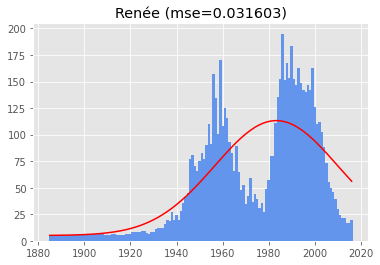
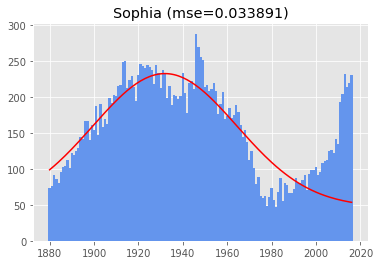
These names look like they might be better modelled using a Mixture of Gaussians, to represent both peaks in popularity.

Note that all one-tailed Gaussians have already been filtered out at this point, as well as uncommon names. If you want to see where your name fits on my somewhat arbitrary Gaussian ranking, I have made a textfile available here.